BINOMIALCDF Function
Evaluates the binomial distribution function.
Usage
result = BINOMIALCDF(k, n, p)
Input Parameters
k—Argument for which the binomial distribution function is to be evaluated.
n—Number of Bernoulli trials.
p—Probability of success on each trial.
Returned Value
result—The probability that k or fewer successes occur in n independent Bernoulli trials, each of which has a probability p of success.
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
Function BINOMIALCDF evaluates the distribution function of a binomial random variable with parameters n and p by summing probabilities of the random variable taking on the specific values in its range. These probabilities are computed by the following recursive relationship:
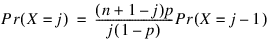
To avoid the possibility of underflow, the probabilities are computed forward from 0 if k is not greater than n times p; otherwise, they are computed backward from n. The smallest positive machine number, ε, is used as the starting value for summing the probabilities, which are rescaled by (1 – p)nε if forward computation is performed and by pnε if backward computation is done.
For the special case of p = 0, BINOMIALCDF is set to 1; for the case p = 1, BINOMIALCDF is set to 1 if k = n and is set to zero otherwise.
Example
Suppose X is a binomial random variable with n = 5 and p = 0.95. This example finds the probability that X is less than or equal to 3.
p = BINOMIALCDF(3, 5, .95)
PM, 'Pr(x < 3) = ', p, Format = '(a12, f7.4)'
; PV-WAVE prints: Pr(x < 3) = 0.0226
Informational Errors
STAT_LESS_THAN_ZERO—Input parameter, k, is less than zero.
STAT_GREATER_THAN_N—Input parameter, k, is greater than the number of Bernoulli trials, n.





