GAMMACDF Function
Evaluates the gamma distribution function.
Usage
result = GAMMACDF(x, a)
Input Parameters
x—Argument for which the gamma distribution function is to be evaluated.
a—Shape parameter of the gamma distribution. This parameter must be positive.
Returned Value
result—The probability that a gamma random variable takes a value less than or equal to x.
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
Function GAMMACDF evaluates the distribution function, F, of a gamma random variable with shape parameter a; that is:
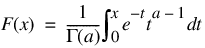
where Γ(·) is the gamma function. (The gamma function is the integral from 0 to infinity of the same integrand as above.) The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive) or even as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over (c, infinity) is as follows:
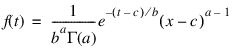
If T is such a random variable with parameters a, b, and c, the probability that T ≤ t0 can be obtained from GAMMACDF by setting x = (t0 – c )/b.
If x is less than a or if x is less than or equal to 1.0, GAMMACDF uses a series expansion; otherwise, a continued fraction expansion is used. (See Abramowitz and Stegun, 1964.)
Example
Let X be a gamma random variable with a shape parameter of 4. (In this case, it has an Erlang distribution, since the shape parameter is an integer.) This example finds the probability that X is less than 0.5 and the probability that X is between 0.5 and 1.0.
a = 4
x = .5
p = GAMMACDF(x, a)
PM, p, Title = 'The probability that X is less than .5 is:'
; PV-WAVE prints the following:
; The probability that X is less than .5 is: 0.00175162
x = 1
p = GAMMACDF(x, a) - p
PM, p, Title = 'The probability that X is between .5 and 1 is:'
; PV-WAVE prints the following:
; The probability that X is between .5 and 1 is: 0.0172365
Informational Errors
STAT_LESS_THAN_ZERO—Input argument, x, is less than zero.
Fatal Errors
STAT_X_AND_A_TOO_LARGE—Function overflows because x and a are too large.





