Evaluates the Student’s t distribution or noncentral Student’s t distribution. Using a keyword the inverse of these distributions can be computed.

t—Argument for which the Student’s t distribution function is to be evaluated. A scalar or 1-dimensional vector.

df—Degrees of freedom. Argument df must be greater than or equal to 1.0.

delta—(Optional) The noncentrality parameter.

result—The probability that a Student’s t random variable takes a value less than or equal to the input t.

Double—If present and nonzero, double precision is used.

Inverse—If present and nonzero, evaluates the inverse of the Student’s t distribution function. If Inverse is specified, argument t represents the probability for which the inverse of the Student’s t distribution function is to be evaluated. In this case, t must be in the open interval (0.0, 1.0).

Function TCDF evaluates the distribution function of a Student’s t random variable with ν = df degrees of freedom. If t2 ≥ ν, the relationship of a t to an F random variable (and subsequently, to a beta random variable) is exploited, and percentage points from a beta distribution are used. Otherwise, the method described by Hill (1970) is used. If ν is not an integer or if ν is greater than 19, a Cornish-Fisher expansion is used to evaluate the distribution function. If ν is less than 20 and |t| is less than 2.0, a trigonometric series (see Abramowitz and Stegun 1964, Equations 26.7.3 and 26.7.4, with some rearrangement) is used. For the remaining cases, a series given by Hill (1970) that converges well for large values of t is used.

If keyword Inverse is specified, the TCDF function evaluates the inverse distribution function of a Student’s t random variable with ν = df degrees of freedom. If ν equals 1 or 2, the inverse can be obtained in closed form. If ν is between 1 and 2, the relationship of a t to a beta random variable is exploited, and the inverse of the beta distribution is used to evaluate the inverse. Otherwise, the algorithm of Hill (1970) is used. For small values of ν greater than 2, Hill’s algorithm inverts an integrated expansion in 1/(1 + t2/ν) of the t density. For larger values, an asymptotic inverse Cornish-Fisher type expansion about normal deviates is used.

Function TCDF evaluates the distribution function F of a noncentral t random variable with df degrees of freedom and noncentrality parameter delta; that is, with v = df, δ = delta , and t0 = t:

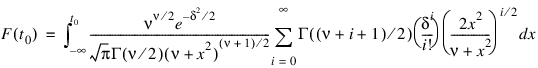
where Γ(·) is the gamma function. The value of the distribution function at the point t0 is the probability that the random variable takes a value less than or equal to t0.

The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi-squared random variable. If w has a normal distribution with mean δ and variance equal to one, u has an independent chi-squared distribution with v degrees of freedom, and:

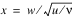
then x has a noncentral t distribution with degrees of freedom and noncentrality parameter δ.

The distribution function of the noncentral t can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The function TNDF uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.

If Inverse is specified TCDF evaluates the inverse distribution function of a noncentral t random variable with df degrees of freedom and noncentrality parameter delta; that is, with P = p, v = df, and δ = delta, it determines t0 (= TCDF(p, df, delta)), such that:

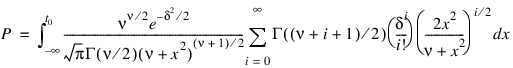
where Γ(·) is the gamma function. The probability that the random variable takes a value less than or equal to t0 is P.

This example finds the probability that a t random variable with six degrees of freedom is greater in absolute value than 2.447. Argument t is symmetric about zero.

p = 2 * TCDF(-2.447, 6)

PM, 'Pr(|t(6)| > 2.447) = ', p, Format = '(a21, f7.4)'

; PV-WAVE prints: Pr(|t(6)| > 2.447) =  0.0500

To use TCDF with arrays that are not 1-dimensional, create a temporary reformed version of your original array before calling TCDF, then reform the return result.

@waveadv

; Create a 3x2 array

array = RANDOMU(seed,3,2)

; Reform the 3x2 array into a 1-dimensional vector

vector = REFORM(array,6)

; Use this 1-dimensional vector as input to FCDF

result_vector = TCDF(vector,8)

; Reform the 1-dimensional vector back into a 3x2 array

result_array = REFORM(result_vector,3,2)

STAT_OVERFLOW—Function TCDF is set to machine infinity since overflow would occur upon modifying the inverse value for the F distribution with the result obtained from the inverse beta distribution.