KAPLAN_MEIER_ESTIMATES Function
Computes Kaplan-Meier estimates of survival probabilities in stratified samples.
Usage
result = kaplan_meier_estimates (x)
Input Parameters
x—Array of size n_observations by ncol. When ncol is 1 the array is one-dimensional. Otherwise it is a two-dimensional array.
Returned Value
result—Array of length n_observations by 2. The first column contains the estimated survival probabilities, and the second column contains Greenwood’s estimate of the standard deviation of these probabilities. If the ith observation contains censor codes out of range or if a variable is missing, then the corresponding elements of the return value are set to missing (NaN, not a number). Similarly, if an element in the return value is not defined, then it is set to missing.
Input Keywords
Double—If present and nonzero, double precision is used.
X_response_col—Column index for the response times in the data array, x. The interpretation of these times as either right-censored or exact failure times depends on Censor_codes_col. Default: X_response_col = 0.
Censor_codes_col—Column index for the optional censoring codes in the data array, x. If x(i, Censor_codes_col) = 0, the failure time x(i, X_response_col) is treated as an exact time of failure. Otherwise it is treated as a right-censored time. Default: It is assumed that there is no censor code column in x. All observations are assumed to be exact failure times.
Freq_response_col—Column index for the number of responses associated with each row in the data array, x. Default: It is assumed that there is no frequency response column in x. Each observation in the data array is assumed to be for a single failure.
Stratum_number_col—Column index for the stratum number for each observation in the data array, x. Column Stratum_number_col of x contains a unique value for each stratum in the data. Kaplan-Meier estimates are computed within each stratum. Default: It is assumed that there is no stratum number column in x. The data is assumed to come from one stratum.
Sorted—If this option is used, column X_response_col of x is assumed to be sorted in ascending order within each stratum. Otherwise, a detached sort is conducted prior to analysis. If sorting is performed, all censored individuals are assumed to follow tied failures. Default: Column X_response_col of x is not sorted.
Output Keywords
N_missing—Number of rows of data in x containing missing values.
Discussion
KAPLAN_MEIER_ESTIMATES computes Kaplan-Meier (or product-limit) estimates of survival probabilities for a sample of failure times that can be right censored or exact times. A survival probability S(t) is defined as 1 – F(t), where F(t) is the cumulative distribution function of the failure times (t). Greenwood’s estimate of the standard errors of the survival probability estimates are also computed. (See Kalbfleisch and Prentice, 1980, pages 13 and 14.)
Let (ti, δi), for i = 1,…, n denote the failure censoring times and the censoring codes for the n observations in a single sample. Here, ti = xi-1, x_response_col is a failure time if δi is 0, where δi = xi-1, censor_codes_col. Also, ti is a right censoring time if δi is 1. Rows in x containing values other than 0 or 1 for δi are ignored. Let the number of observations in the sample that have not failed by time s(ι) be denoted by n(ι), where s(ι) is an ordered (from smallest to largest) listing of the distinct failure times (censoring times are omitted). Then the Kaplan-Meier estimate of the survival probabilities is a step function, which in the interval from s(ι) to s(i+1) (including the lower endpoint) is given by:
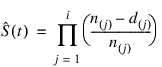
where d(j) denotes the number of failures occurring at time s(j), and n(ϕ) is the number of observation that have not failed prior to s(j).
Note that one row of x may correspond to more than one failed (or censored) observation when the frequency option is in effect (Freq_response_col is specified). The Kaplan-Meier estimate of the survival probability prior to time s(1) is 1.0, while the Kaplan-Meier estimate of the survival probability after the last failure time is not defined.
Greenwood’s estimate of the variance of:
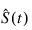
in the interval from s(i) to s(i + 1) is given as:
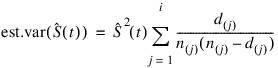
KAPLAN_MEIER_ESTIMATES computes the single sample estimates of the survival probabilities for all samples of data included in x during a single call. This is accomplished through the Stratum_number_col column of x, which if present, must contain a distinct code for each sample of observations. If Stratum_number_col is not specified, there is no grouping column, and all observations are assumed to come from the same sample.
When failures and right-censored observations are tied and the data is to be sorted by KAPLAN_MEIER_ESTIMATES (Sorted keyword is not used), KAPLAN_MEIER_ESTIMATES assumes that the time of censoring for the tied-censored observations is immediately after the tied failure (within the same sample). When the Sorted keyword is used, the data is assumed to be sorted from smallest to largest according to column X_response_col of x within each stratum. Furthermore, a small increment of time is assumed (theoretically) to elapse between the failed and censored observations that are tied (in the same sample). Thus, when the Sorted keyword is used, the user must sort all of the data in x from smallest to largest according to column X_response_col (and column Stratum_number_col, if present). By appropriate sorting of the observations, the user can handle censored and failed observations that are tied in any manner desired.
Example
The following example is taken from Kalbfleisch and Prentice (1980, page 1). The first column in x contains the death/censoring times for rats suffering from vaginal cancer. The second column contains information as to which of two forms of treatment were provided, while the third column contains the censoring code. Finally, the fourth column contains the frequency of each observation. The product-limit estimates of the survival probabilities are computed for both groups with one call to KAPLAN_MEIER_ESTIMATES.
KAPLAN_MEIER_ESTIMATES could have been called with the Sorted keyword if the censored observations had been sorted with respect to the failure time variable.
; Column index for the optional censoring codes in data x
censor_codes_col = 2
; Column index for the number of responses
; associated with each row in data x.
freq_response_col = 3
; Column index for the stratum number for each
; observation in data x
stratum_number_col = 1
; Number of columns in x.
ncol = 4
; Number of observations.
n_observations = 33
; Two-dimensional data array of size n_observations*ncol
x = [ 143, 5, 0, 1, $
164, 5, 0, 1, $
188, 5, 0, 2, $
190, 5, 0, 1, $
192, 5, 0, 1, $
206, 5, 0, 1, $
209, 5, 0, 1, $
213, 5, 0, 1, $
216, 5, 0, 1, $
220, 5, 0, 1, $
227, 5, 0, 1, $
230, 5, 0, 1, $
234, 5, 0, 1, $
246, 5, 0, 1, $
265, 5, 0, 1, $
304, 5, 0, 1, $
216, 5, 1, 1, $
244, 5, 1, 1, $
142, 7, 0, 1, $
156, 7, 0, 1, $
163, 7, 0, 1, $
198, 7, 0, 1, $
205, 7, 0, 1, $
232, 7, 0, 2, $
233, 7, 0, 4, $
239, 7, 0, 1, $
240, 7, 0, 1, $
261, 7, 0, 1, $
280, 7, 0, 2, $
296, 7, 0, 2, $
323, 7, 0, 1, $
204, 7, 1, 1, $
344, 7, 1, 1]
; Reforming data to match input requirements
x = TRANSPOSE(REFORM(x, ncol, n_observations))
;
; Call the KAPLAN_MEIER_ESTIMATES routine
;
r = KAPLAN_MEIER_ESTIMATES(x, $
Freq_response_col=freq_response_col, $
Censor_codes_col=censor_codes_col, $
Stratum_number_col=stratum_number_col)
;
; Print the output
PRINT," Survival Estimated"
PRINT," Probability Std. Error"
FOR i=0L, n_observations - 1 DO $
PRINT, r(i,0), r(i,1)
Output
Survival Estimated
Probability Std. Error
0.947368 0.0512278
0.894737 0.0704059
0.789474 0.0935288
0.736842 0.101023
0.684210 0.106639
0.631579 0.110665
0.578947 0.113269
0.526316 0.114549
0.473684 0.114549
0.414474 0.114515
0.355263 0.112426
0.296053 0.108162
0.236842 0.101450
0.157895 0.0934313
0.0789474 0.0727921
0.00000 NaN
0.473684 0.114549
0.236842 0.101450
0.952381 0.0464714
0.904762 0.0640564
0.857143 0.0763604
0.809524 0.0856891
0.758929 0.0940923
0.657738 0.105295
0.455357 0.111368
0.404762 0.109887
0.354167 0.107168
0.303571 0.103112
0.202381 0.0902139
0.101190 0.0677829
0.0505952 0.0492805
0.809524 0.0856891
NaN NaN





