FAURE_INIT Function
Initializes the structure used for computing a shuffled Faure sequence.
Usage
result = FAURE_INIT(ndim)
Input Parameters
ndim—The dimension of the hyper-rectangle.
Returned Value
A structure that contains information about the sequence.
Input Keywords
Base—The base of the Faure sequence. Default: The smallest prime greater than or equal to ndim.
Skip—The number of points to be skipped at the beginning of the Faure sequence. Default:
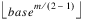
where:
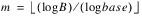
and B is the largest representable integer.
Discussion
Discrepancy measures the deviation from uniformity of a point set.
The discrepancy of the point set:
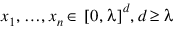
is:
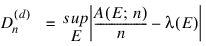
where the supremum is over all subsets of [0, λ]d of the form:
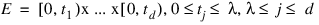
λ is the Lebesque measure, and:
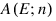
is the number of the xj contained in E.
The sequence x1, x2, … of points [0,λ]d is a low-discrepancy sequence if there exists a constant c(d), depending only on d, such that:
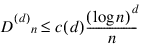
for all n>1.
Generalized Faure sequences can be defined for any prime base b≥d. The lowest bound for the discrepancy is obtained for the smallest prime b≥d, so the keyword Base defaults to the smallest prime greater than or equal to the dimension.
The generalized Faure sequence x1, x2, …, is computed as follows:
Write the positive integer n in its b-ary expansion:
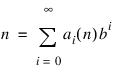
where ai (n) are integers:
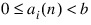
The jth coordinate of xn is:
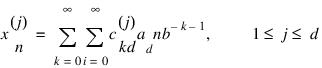
The generator matrix for the series:
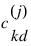
is defined to be:
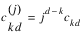
and:
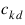
is an element of the Pascal matrix:
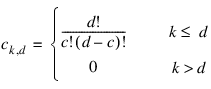
It is faster to compute a shuffled Faure sequence than to compute the Faure sequence itself. It can be shown that this shuffling preserves the low-discrepancy property.
The shuffling used is the b-ary Gray code. The function G(n) maps the positive integer n into the integer given by its b-ary expansion.
The sequence computed by this function is x(G(n)), where x is the generalized Faure sequence.
Example
In this example, five points in the Faure sequence are computed. The points are in the three-dimensional unit cube.
Note that FAURE_INIT is used to create a structure that holds the state of the sequence. Each call to FAURE_NEXT_PT returns the next point in the sequence and updates the state structure.
state = FAURE_INIT(3)
p = FAURE_NEXT_PT(5, state)
PM, p
; This results in the following output:
; 0.333689 0.492659 0.0640654
; 0.667022 0.825992 0.397399
; 0.778133 0.270436 0.175177
; 0.111467 0.603770 0.508510
; 0.444800 0.937103 0.841843





