Evaluates the price, per $100 face value, of a security that pays interest at maturity.

settlement—The date on which payment is made to settle a trade. For a more detailed discussion on dates see Chapter 8, Working with Date/Time Data in the .

maturity—The date on which the bond comes due, and principal and accrued interest are paid. For a more detailed discussion on dates see Chapter 8, Working with Date/Time Data in the .

issue—The date on which interest starts accruing. For a more detailed discussion on dates see Chapter 8, Working with Date/Time Data in the .

rate—Annual interest rate set forth on face of the security; coupon rate.

yield—Annual yield of the security.

basis—The method for computing the number of days between two dates. It should be 0, 1, 2, 3, or 4.

result—The price per $100 face value of a security that pays interest at maturity. If no result can be computed, NaN is returned.

Double—If present and nonzero, double precision is used.

Function PRICE_MATURITY computes the price per $100 face value of a security that pays interest at maturity.

It is computed using the following:

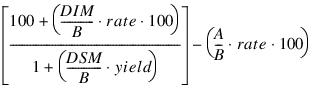
In the equation above, B represents the number of days in a year based on the annual basis. DSM represents the number of days in the period starting with the settlement date and ending with the maturity date. DIM represents the number of days in the period starting with the issue date and ending with the maturity date. A represents the number of days in the period starting with the issue date and ending with the settlement date.

In this example, PRICE_MATURITY computes the price at maturity of a security with the settlement date of August 1, 2000, maturity date of July 1, 2001 and issue date of July 1, 2000, using the US (NASD) 30/360 day count method. The security has 5% annual yield and 5% interest rate at the date of issue.

settlement = VAR_TO_DT(2000, 8, 1)

maturity = VAR_TO_DT(2001, 7, 1)

issue = VAR_TO_DT(2000, 7, 1)

rate = .05

yield = .05

basis = 1

PRINT, PRICE_MATURITY(settlement, maturity, issue, $

   rate, yield, basis)

; PV-WAVE prints: 99.9817