BESSK Function
Evaluates a modified Bessel function of the second kind with real order and real or complex parameters.
Usage
result = BESSK(order, z)
Input Parameters
order—Real parameter specifying the desired order. Parameter order must be greater than –1/2.
z—Real or complex parameter for which the Bessel function is to be evaluated.
Returned Value
result—The desired value of the modified Bessel function.
Input Keywords
Double—If present and nonzero, double precision is used.
Sequence—If present and nonzero, a one-dimensional array of length n containing the values of the Bessel function through the series is returned by BESSK, where n = NELEMENTS(Sequence). The ith element of this array is the Bessel function of order (order + i) at z for i = 0, ... (n – 1).
Discussion
Function BESSK evaluates a modified Bessel function of the second kind with real order and real or complex parameters. The data type of the returned value is always complex.
The Bessel function, Kv(z), is defined as follows:
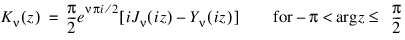
This function is based on the code BESSCC of Thompson (1981) and Thompson and Barnett (1987). For moderate or large parameters, z, Temme’s (1975) algorithm is used to find Kv (z). This involves evaluating a continued fraction. If this evaluation fails to converge, the answer may not be accurate. For small z, a Neumann series is used to compute Kv (z). Upward recurrence of the Kv (z) is always stable.
Example
In this example, K0.3 + v–1(1.2 + 0.5i), v = 1, ..., 4 is computed and printed.
z = COMPLEX(1.2, .5)
FOR i=0L, 3 DO PM, BESSK(i + .3, z) ; PV-WAVE prints:
; ( 0.245546, -0.199599)
; ( 0.335637, -0.362005)
; ( 0.586718, -1.12610)
; ( 0.719457, -4.83864)
PM, BESSK(.3, z, Sequence = 4), Title = 'With SEQUENCE:'
; PV-WAVE prints the following:
; With SEQUENCE:
; ( 0.245546, -0.199599)
; ( 0.335637, -0.362005)
; ( 0.586718, -1.12610)
; ( 0.719456, -4.83864)





