BESSI Function
Evaluates a modified Bessel function of the first kind with real order and real or complex parameters.
Usage
result = BESSI(order, z)
Input Parameters
order—Real parameter specifying the desired order. Parameter order must be greater than –1/2.
z—Real or complex parameter for which the Bessel function is to be evaluated.
Returned Value
result—The desired value of the modified Bessel function.
Input Keywords
Double—If present and nonzero, double precision is used.
Sequence—If present and nonzero, a one-dimensional array of length n containing the values of the Bessel function through the series is returned by BESSI, where n = N_ELEMENTS(Sequence). The ith element of this array is the Bessel function of order (order + i) at z for i = 0, ... (n – 1).
Discussion
Function BESSI evaluates a modified Bessel function of the first kind with real order and real or complex parameters. The data type of the returned value is always complex.
The Bessel function, Iv(z), is defined as follows:
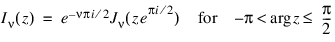
For large parameters, z, Temme’s (1975) algorithm is used to find Iv(z). The Iv(z) values are recurred upward (if stable). This involves evaluating a continued fraction. If this evaluation fails to converge, the answer may not be accurate. For moderate and small parameters, Miller’s method is used.
Example
In this example, J0.3 + v–1(1.2 + 0.5i), v = 1, ... 4 is computed and printed first by calling BESSI four times in a row, then by using the keyword Sequence.
z = COMPLEX(1.2, .5)
FOR i=0L, 3 DO PM, BESSI(i + .3, z)
; PV-WAVE prints the following:
; ( 1.16339, 0.396301)
; ( 0.447264, 0.332142)
; ( 0.0821799, 0.127165)
; ( 0.00577678, 0.0286277)
PM, BESSI(.3, z, Sequence = 4), Title = 'With SEQUENCE:'
; PV-WAVE prints the following:
; With SEQUENCE:
; ( 1.16339, 0.396301)
; ( 0.447264, 0.332142)
; ( 0.0821799, 0.127165)
; ( 0.00577678, 0.0286277)