GAMMA Function
Evaluates the real gamma function Γ(x).
Usage
result = GAMMA(x)
Input Parameters
x—Expression for which the gamma function is to be evaluated.
Returned Value
result—The value of the gamma function Γ(x).
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
The gamma function, Γ(x), is defined as follows:
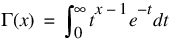
For x < 0, the above definition is extended by analytic continuation.
The gamma function is not defined for integers less than or equal to zero. It underflows for:
x << 0
and overflows for large x. It also overflows for values near negative integers.
Example
In this example, Γ(1.5) is computed and printed.
PM, GAMMA(1.5) ; PV-WAVe prints: 0.886227
Alert Errors
MATH_SMALL_ARG_UNDERFLOW—Parameter x must be large enough that Γ(x) does not underflow. The underflow limit occurs first for parameters close to large negative half integers. Even though other parameters away from these half integers may yield machine-representable values of Γ(x), such parameters are considered illegal. Users who need such values should use the log Γ(x) function LNGAMMA.
Warning Errors
MATH_NEAR_NEG_INT_WARN—Result is accurate to less than one-half precision because x is too close to a negative integer.
Fatal Errors
MATH_ZERO_ARG_OVERFLOW—Parameter for the gamma function is too close to zero.
MATH_NEAR_NEG_INT_FATAL—Parameter for the function is too close to a negative integer.
MATH_LARGE_ARG_OVERFLOW—Function overflows because x is too large.
MATH_CANNOT_FIND_XMIN—Algorithm used to find xmin failed. This error should never occur.
MATH_CANNOT_FIND_XMAX—Algorithm used to find xmax failed. This error should never occur.





