K_MEANS Function
Performs a K-means (centroid) cluster analysis.
Usage
result = K_MEANS(x, seeds)
Input Parameters
x—Two-dimensional array containing observations to be clustered. The data value for the ith observation of the jth variable should be in x(i, j).
seeds—Two-dimensional array containing the cluster seeds, i.e., estimates for the cluster centers. The seed value for the jth variable of the ith seed should be in seeds (i, j).
Returned Value
result—The cluster membership for each observation is returned.
Input Keywords
Double—If present and nonzero, double precision is used.
Weights—One-dimensional array containing the weight of each observation of matrix x. Default: Weights(*) = 1
Frequencies—One-dimensional array containing the frequency of each observation of matrix x. Default: Frequencies(*) = 1
Itmax—Maximum number of iterations. Default: Itmax = 30
Var_Columns—One-dimensional array containing the columns of x to be used in computing the metric. Columns are numbered 0, 1, 2, ..., N_ELEMENTS(x(0, *)). Default: Vars_Columns(*) = 0, 1, 2, ..., N_ELEMENTS(x(0, *)) – 1
Output Keywords
Means_Cluster—Named variable into which a two-dimensional array containing the cluster means is stored.
Ssq_Cluster—Named variable into which a one-dimensional array containing the within sum-of-squares for each cluster is stored.
Counts_Cluster—Named variable into which an array containing the number of observations in each cluster is stored.
Discussion
Function K_MEANS is an implementation of Algorithm AS 136 by Hartigan and Wong (1979). This function computes K-means (centroid) Euclidean metric clusters for an input matrix starting with initial estimates of the K-cluster means. The K_MEANS function allows for missing values coded as NaN (Not a Number) and for weights and frequencies.
Let p = N_ELEMENTS(x (0, *)) be the number of variables to be used in computing the Euclidean distance between observations. The idea in K-means cluster analysis is to find a clustering (or grouping) of the observations so as to minimize the total within-cluster sums-of-squares. In this case, the total sums-of-squares within each cluster is computed as the sum of the centered sum-of-squares over all nonmissing values of each variable. That is:
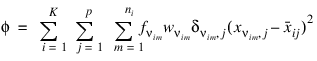
where νim denotes the row index of the mth observation in the ith cluster in the matrix X; ni is the number of rows of X assigned to group i; f denotes the frequency of the observation; w denotes its weight; δ is 0 if the jth variable on observation νim is missing, otherwise δ is 1; and:
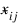
is the average of the nonmissing observations for variable j in group i. This method sequentially processes each observation and reassigns it to another cluster if doing so results in a decrease of the total within-cluster sums-of-squares. See Hartigan and Wong (1979) or Hartigan (1975) for details.
Example
This example performs K-means cluster analysis on Fisher’s iris data, which is obtained by function STATDATA. The initial cluster seed for each iris type is an observation known to be in the iris type.
seeds = MAKE_ARRAY(3,4)
; Use Columns 1, 2, 3, and 4 of data matrix x, only.
x = STATDATA(3)
seeds(0, *) = x(0, 1:4)
seeds(1, *) = x(50, 1:4)
seeds(2, *) = x(100, 1:4)
cluster_group = K_MEANS(x(*, 1:4), seeds, $
Means_Cluster = means_cluster, Ssq_Cluster = ssq_cluster, $
Counts_Cluster = counts_cluster)
format = '(a, 10i4)'
; Print cluster membership in groups of 10.
FOR i=0L, 140, 10 DO BEGIN &$
PRINT, 'observation: ',i + INDGEN(10)+1, $
Format = format &$
PRINT, 'cluster: ', cluster_group(i:i+9), $
Format = format &$
PRINT &$
END
; PV-WAVE prints the following:
; observation: 1 2 3 4 5 6 7 8 9 10
; cluster : 1 1 1 1 1 1 1 1 1 1
; observation: 11 12 13 14 15 16 17 18 19 20
; cluster : 1 1 1 1 1 1 1 1 1 1
; observation: 21 22 23 24 25 26 27 28 29 30
; cluster : 1 1 1 1 1 1 1 1 1 1
; observation: 31 32 33 34 35 36 37 38 39 40
; cluster : 1 1 1 1 1 1 1 1 1 1
; observation: 41 42 43 44 45 46 47 48 49 50
; cluster : 1 1 1 1 1 1 1 1 1 1
; observation: 51 52 53 54 55 56 57 58 59 60
; cluster : 2 2 3 2 2 2 2 2 2 2
; observation: 61 62 63 64 65 66 67 68 69 70
; cluster : 2 2 2 2 2 2 2 2 2 2
; observation: 71 72 73 74 75 76 77 78 79 80
; cluster : 2 2 2 2 2 2 2 3 2 2
; observation: 81 82 83 84 85 86 87 88 89 90
; cluster : 2 2 2 2 2 2 2 2 2 2
; observation: 91 92 93 94 95 96 97 98 99 100
; cluster : 2 2 2 2 2 2 2 2 2 2
; observation: 101 102 103 104 105 106 107 108 109 110
; cluster : 3 2 3 3 3 3 2 3 3 3
; observation: 111 112 113 114 115 116 117 118 119 120
; cluster : 3 3 3 2 2 3 3 3 3 2
; observation: 121 122 123 124 125 126 127 128 129 130
; cluster : 3 2 3 2 3 3 2 2 3 3
; observation: 131 132 133 134 135 136 137 138 139 140
; cluster : 3 3 3 2 3 3 3 3 2 3
; observation: 141 142 143 144 145 146 147 148 149 150
; cluster : 3 3 2 3 3 3 2 3 3 2
PM, [[INDGEN(3) + 1],[means_cluster]], Title = 'Cluster Means:',$
Format = '(i3, 5x, 4f8.4)'
; PV-WAVE prints the following:
; Cluster Means:
; 1 5.0060 3.4280 1.4620 0.2460
; 2 5.9016 2.7484 4.3935 1.4339
; 3 6.8500 3.0737 5.7421 2.0711
PM, [[INDGEN(3) + 1],[ssq_cluster]], $
Title = 'Cluster Sums of Squares:', Format = '(i3, 5x, f8.4)'
; PV-WAVE prints the following:
; Cluster Sums of Squares:
; 1 15.1510
; 2 39.8210
; 3 23.8795
PM, [[INDGEN(3) + 1],[counts_cluster]], Title = $
'Number of Observations per Cluster:'
; PV-WAVE prints the following:
; Number of Observations per Cluster:
; 1 50
; 2 62
; 3 38
Warning Errors
STAT_NO_CONVERGENCE—Convergence did not occur.





