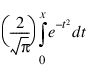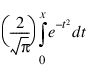ERRORF Function
Calculates the standard error function of the input variable.
Usage
result = ERRORF(x)
Input Parameters
x—The vector for which the error function will be evaluated.
Returned Value
result—The standard error function of x. It is of floating-point data type, and has the same dimensions as x.
Keywords
None.
Discussion
The standard error function is central to many calculations in statistics. The ERRORF function can be used in a variety of applications; one example is to solve diffusion equations in heat transfer problems. The error function is a special case of the incomplete gamma function. ERRORF is defined as:
ERRORF has the following limiting values and symmetries:
erf(0) = 0
erf(∞) = 1
erf(-x) = –erf(x)
It is related to the incomplete gamma function by:
erf(x) = Γ(1/2, x2)
where x ≥ 0.
See Also
The method used to determine the error function of complex operands is taken from: W. Gautschi, “Efficient computation of the complex error function,” Siam Journal of Numerical Analysis, Volume 7, page 187, 1970.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.