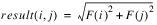DIST Function

Reference Guide > D Routines > DIST Function

DIST Function

Standard Library function that generates a square array in which each element equals the Euclidean distance from the nearest corner.

Usage

result = DIST(n, [m])

Input Parameters

n — The size of the resulting array.

m — If this parameter is supplied, the function generates a rectangular Euclidean distance array.

Returned Value

result — The resulting floating-point array.

Keywords

None.

Discussion

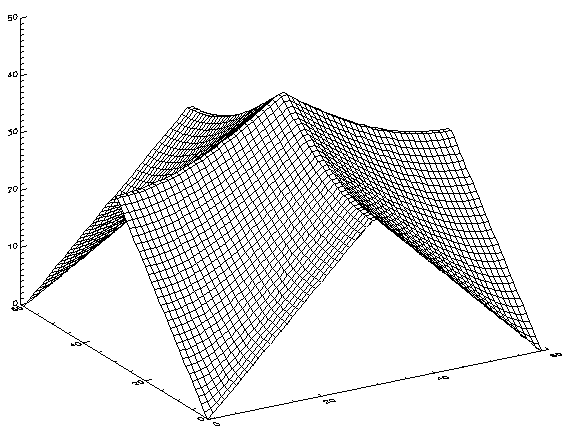
DIST generates a square array in which each element is proportional to its frequency. A three-dimensional plot of this function displays a surface where each quadrant is a curved quadrilateral forming a common cusp at the center.

The result of the DIST function is an n-by-n single-precision floating-point array, as defined by:

where:

F(x) = x if 0 ≤ x < n/2

or:

F(x) = n – 1 – x if x ≥ n/2

The DIST function is particularly useful for creating arrays that can be used for frequency domain filtering in image and signal processing applications.

note	DIST is an excellent choice when you need a two-dimensional array of any size for a fast test display.

If the optional parameter m is supplied, the result is an n-by-m rectangular Euclidean distance array.

Example 1

Use the commands:

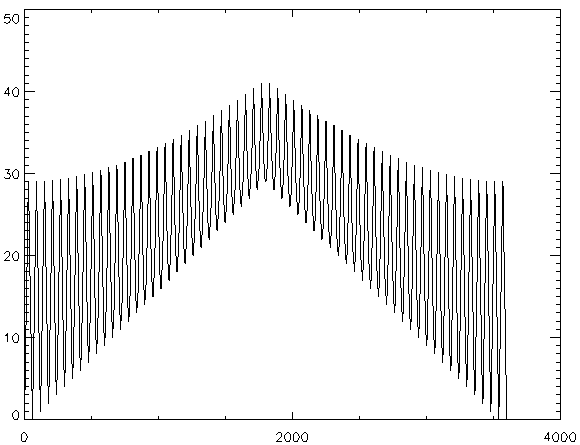
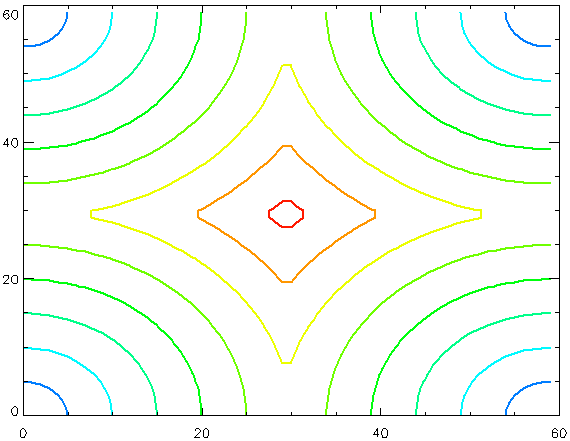
test_arr = DIST(60)

LOADCT, 18

; Display data as a 2D plot

WINDOW, /Free

PLOT, test_arr, Background=WoColorConvert(255), Color=WoColorConvert(0)

; Display data as a contour plot

WINDOW, /Free

CONTOUR, test_arr, Background=WoColorConvert(255), Color=WoColorConvert(0), $

   Thick=2.0, Nlevels=9, $

   C_Colors=WoColorConvert([50, 75, 100, 125, 150, 175, 200, 225, 250])

; Display data as a surface

WINDOW, /Free

SURFACE, test_arr, Linestyle=2, Background=WoColorConvert(255), $

   Color=WoColorConvert(0)

; Display data as a shaded surface

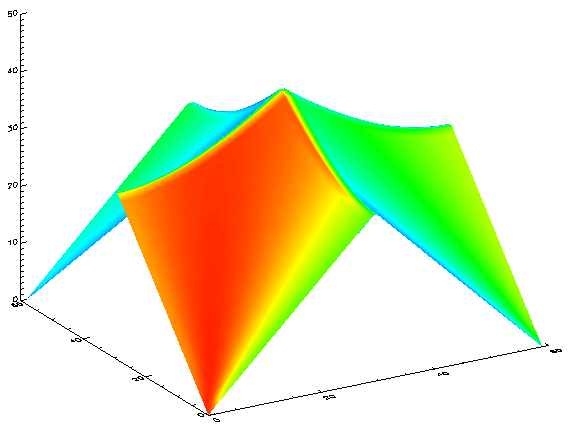
WINDOW, /Free

SHADE_SURF, test_arr, Background=WoColorConvert(255), Color=WoColorConvert(0)

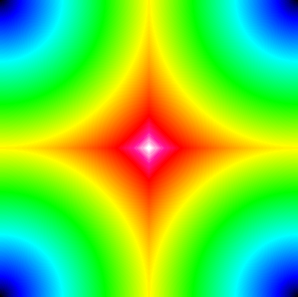
; Display data as an image

test_img = DIST(300)

WINDOW, Xsize=300, Ysize=300, /Free

TVSCL, test_img, 3

to create an array and display that array using multiple methods. The results are shown in the following images.

Figure 5-4: 2D Plot

Figure 5-5: Contour Plot

Figure 5-6: Surface

Figure 5-7: Shaded Surface

Figure 5-8: Image

Example 2

This example shows how to use the DIST function to filter an image.

; Read the demo image.

mandril = BYTARR(512,512)

OPENR, unit, !Data_dir + 'mandril.img', /Get_lun

READU, unit, mandril

FREE_LUN, unit

; Use the DIST function to create a frequency image of the same

; size as the demo image.

d = DIST(512)

; Set n, the order (steepness) of Butterworth filter to use, and

; d0, the cutoff frequency.

n = 1.0

d0 = 10.0

; Create a Butterworth low-pass filter to be applied to the image.

filter = 1.0 / (1.0 + (d/d0)^(2.0 * n))

; Filter the image by transforming it to the frequency domain,

; multiplying by the filter, and then transforming back to the

; spatial domain.

filt_image = FFT(FFT(mandril, -1) * filter, 1)

; Display the original image.

WINDOW, XSize=1024, YSize=512, /Free, $

   Title='Original Image (left) - Filtered Image (right)'

TVSCL, mandril, 2

; Display the resulting image.

TVSCL, filt_image, 1