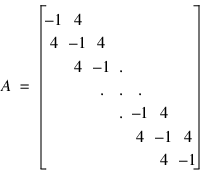Solves a general band system of linear equations Ax = b. Using keywords, any of several related computations can be performed.

b—One-dimensional matrix containing the right-hand side.

nlca—Number of lower codiagonals in a.

nuca—Number of upper codiagonals in a.

a—(Optional) Array of size (nlca + nuca + 1) × n containing the n × n banded coefficient matrix in band storage mode A(i, j). See the chapter introduction for a description of band storage mode.

result—A one-dimensional array containing the solution of the linear system Ax = b.

Transpose—If present and nonzero, ATx = b is solved.

Blk_factor—The blocking factor. This keyword must be set no larger than 32. Default: Blk_factor = 1.

Pivot—One-dimensional array containing the pivot sequence. The keywords Pivot and Factor must be used together. Keywords Pivot and Condition cannot be used together.

Factor—An array of size (2*nlca + nuca + 1) × N_ELEMENTS(b) containing the LU factorization of A with column pivoting, as returned from SP_BDFAC. The keywords Pivot and Factor must be used together. Keywords Factor and Condition cannot be used together.

Double—If present and nonzero, double precision is used.

Condition—Specifies a named variable into which an estimate of the L1 condition number is stored. This keyword cannot be used with Pivot and Factor.

The function SP_BDSOL solves a system of linear algebraic equations with a real or complex band matrix A. It first computes the LU factorization of A with based on the blocked LU factorization algorithm given in Du Croz, et al, (1990). Level-3 BLAS invocations were replaced by in-line loops. The blocking factor Blk_factor has the default value of 1, but can be reset to any positive value not exceeding 32.

The solution of the linear system is then found by solving two simpler systems, y = L–1b and x = U–1y. When the solution to the linear system or the inverse of the matrix is sought, an estimate of the L1 condition number of A is computed using Higham’s modifications to Hager’s method, as given in Higham (1988). If the estimated condition number is greater than 1/ε (where ε is the machine precision), a warning message is issued. This indicates that very small changes in A may produce large changes in the solution x. The function SP_BDSOL fails if U, the upper triangular part of the factorization, has a zero diagonal element.

Consider the 1000 × 1000 banded matrix below:

In this example we compute the solution to Ax = b, where b is a random vector.

n_rows = 1000L

nlca = 1L

nuca = 1L

; Fill A with the values of the bands.

a = DBLARR(n_rows*(nlca+nuca+1))

a(1:n_rows-1) = 4

a(n_rows:2*n_rows-1) = -1

a(2*n_rows:*) = 4

seed = 123L

; Compute a random right-hand side.

b = RANDOMU(seed, n_rows)

; Compute the solution using SP_BDSOL above, and output residual.

x = SP_BDSOL(b, nlca, nuca, a)

PM, TOTAL(ABS(SP_MVMUL(n_rows, n_rows, nlca, nuca, a, x)-b))

; PV-WAVE prints: 1.2367884e-13

SP_BDFAC