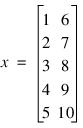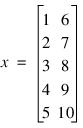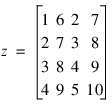TIME_SERIES_FILTER Function (PV-WAVE Advantage)
Converts time series data to the format required for processing by a neural network.
Usage
z = TIME_SERIES_FILTER(max_lag, x)
Input Parameters
max_lag—Scalar value indicating the number of lags, max_lag ≥ 0.
x—Array of size n_obs by n_var, where n_obs is the number of observations and n_var is the number of variables (columns) in x. All data must be sorted in chronological order from most recent to oldest observations.
Returned Value
z—A 2D array of size (n_obs–max_lag) by n_var * (max_lag+1)).
Input Keywords
Double—If present and nonzero, double precision is used.
Discussion
TIME_SERIES_FILTER accepts a data matrix and lags every column to form a new data matrix. The input matrix, x, contains n_var columns. Each column is transformed into (max_lag+1) columns by lagging its values.
Since a lag of zero is always included in the output matrix z, the total number of lags is N_lags = max_lag+1.
The output data array, z, can be represented symbolically as:
z = |x(0) : x(1) : x(2) : … : x(max_lag)|,
where x(i) is the ith lag of the incoming data matrix, x. For example, if x = {1, 2, 3, 4, 5} and n_var = 1, then n_obs = 5, and x(0) = x, x(1)={2, 3, 4, 5}, x(2) = {3, 4, 5}, and so forth.
Consider, an example in which n_obs = 5 and n_var = 2 with all variables continuous input attributes. It is assumed that the most recent observations are in the first row and the oldest are in the last row:
If max_lag = 1, then the number of columns will be n_var*(max_lag+1) = 2 * 2 = 4, and the number of rows will be n_obs – max_lag = 5 – 1 = 4:
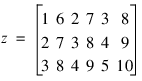
If max_lag = 2, then the number of columns will be n_var * (max_lag + 1) = 2 * 3 = 6. , and the number of rows will be n_obs – max_lag = 5 – 2 = 3:
Example
In this example, the matrix x with 5 rows and 2 columns is lagged twice, i.e. max_lag=2. This produces an output two-dimensional matrix with 5(n_obs – max_lag)= 5 – 2 = 3 rows, but 2*3 = 6 columns. The first two columns correspond to lag = 0, which simply places the original data into these columns. The 3rd and 4th columns contain the first lags of the original 2 columns and the 5th and 6th columns contain the second lags. Note that the number of rows for the output matrix z is less than the number for the input matrix x.
; Number of observations.
n_obs = 5
; Number of variables(column) in x.
n_var = 2
; The number of lags.
max_lag = 2
; An array of size n_obs by n_var.
x = FLOAT([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
; X must be an (n_obs X n_var) float/double array.
x = REFORM(x, n_obs, n_var)
z = TIME_SERIES_FILTER( max_lag, x )
PRINT, ""
PM, FIX(x), Title = "X"
PRINT, ""
PM, FIX(z), Title = "Z"
Output
X
1 6
2 7
3 8
4 9
5 10
Z
1 6 2 7 3 8
2 7 3 8 4 9
3 8 4 9 5 10
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.