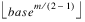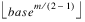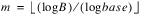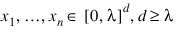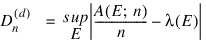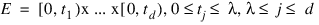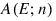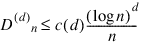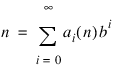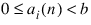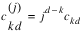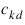FAURE_INIT Function (PV-WAVE Advantage)

Initializes the structure used for computing a shuffled Faure sequence.

ndim—The dimension of the hyper-rectangle.

A structure that contains information about the sequence.

Base—The base of the Faure sequence. Default: The smallest prime greater than or equal to ndim.

Skip—The number of points to be skipped at the beginning of the Faure sequence. Default:

and B is the largest representable integer.

Discrepancy measures the deviation from uniformity of a point set.

The discrepancy of the point set:

where the supremum is over all subsets of [0, λ]d of the form:

λ is the Lebesque measure, and:

is the number of the xj contained in E.

The sequence x1, x2, … of points [0,λ]d is a low-discrepancy sequence if there exists a constant c(d), depending only on d, such that:

Generalized Faure sequences can be defined for any prime base b≥d. The lowest bound for the discrepancy is obtained for the smallest prime b≥d, so the keyword Base defaults to the smallest prime greater than or equal to the dimension.

The generalized Faure sequence x1, x2, …, is computed as follows:

Write the positive integer n in its b-ary expansion:

where ai (n) are integers:

The jth coordinate of xn is:

The generator matrix for the series:

is an element of the Pascal matrix:

It is faster to compute a shuffled Faure sequence than to compute the Faure sequence itself. It can be shown that this shuffling preserves the low-discrepancy property.

The shuffling used is the b-ary Gray code. The function G(n) maps the positive integer n into the integer given by its b-ary expansion.

The sequence computed by this function is x(G(n)), where x is the generalized Faure sequence.

In this example, five points in the Faure sequence are computed. The points are in the three-dimensional unit cube.

Note that FAURE_INIT is used to create a structure that holds the state of the sequence. Each call to FAURE_NEXT_PT returns the next point in the sequence and updates the state structure.