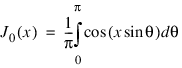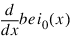KELVIN_BEI0 Function (PV-WAVE Advantage)
Evaluates the Kelvin function of the first kind, bei, of order zero.
Usage
result = KELVIN_BEI0(x)
Input Parameters
x—Argument for which the function value is desired.
Returned Value
result—The value of the Kelvin function of the first kind, bei, of order zero evaluated at x.
Input Keywords
Double—If present and nonzero, double precision is used.
Derivative—If present and nonzero, then the derivative of the Kelvin function of the first kind, bei, of order zero evaluated at x is computed.
Discussion
The Kelvin function bie
0(
x) is defined to be
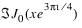
. The Bessel function
J0(
x) is defined:
In KELVIN_BEI0, x must be less than 119.
If the keyword Derivative is set, the function bei0'(x) is defined to be:
If the keyword Derivative is set and |x| > 119, NaN is returned.
The function KELVIN_BEI0 is based on the work of Burgoyne (1963).
Example
In this example, bei0(0.4) and bei0'(0.6) are evaluated.
PRINT, KELVIN_BEI0(0.4)
; PV-WAVE prints: 0.0399982
PRINT, KELVIN_BEI0(0.6, /DERIVATIVE)
; PV-WAVE prints: 0.299798
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.
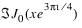 . The Bessel function J0(x) is defined:
. The Bessel function J0(x) is defined: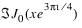 . The Bessel function J0(x) is defined:
. The Bessel function J0(x) is defined: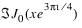 . The Bessel function J0(x) is defined:
. The Bessel function J0(x) is defined: