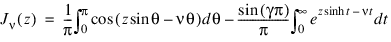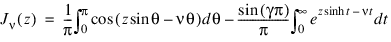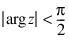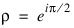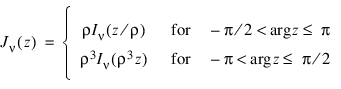BESSJ Function (PV-WAVE Advantage)
Evaluates a Bessel function of the first kind with real order and real or complex parameters.
Usage
result = BESSJ(order, z)
Input Parameters
order—Real parameter specifying the desired order. Parameter order must be greater than –1/2.
z—Real or complex parameter to evaluate the Bessel function for.
Returned Value
result—The desired value of the Bessel function.
Input Keywords
Double—If present and nonzero, double precision is used.
Sequence—If present and nonzero, a one-dimensional array of length n containing the values of the Bessel function through the series is returned by BESSJ, where n = NELEMENTS(Sequence). The ith element of this array is the Bessel function of order (order + i) at z for i = 0, ... (n – 1).
Discussion
Function BESSJ evaluates a Bessel function of the first kind with real order and real or complex parameters. The data type of the returned value is always complex.
The Bessel function, Jv(z), is defined as follows:
for:
This function is based on the code BESSCC of Barnett (1981) and Thompson and Barnett (1987). This code computes Jv(z) from the modified Bessel function Iv(z), using the following relation with:
Example
In this example, J0.3 + v–1(1.2 + 0.5i), v = 1, ..., 4 is computed and printed.
z = COMPLEX(1.2, .5)
FOR i=0L, 3 DO PM, BESSJ(i + .3, z)
; PV-WAVE prints the following:
; ( 0.773756, -0.106925)
; ( 0.400001, 0.158598)
; ( 0.0867063, 0.0920276)
; ( 0.00844932, 0.0239868)
PM, BESSJ(.3, z, Sequence = 4), Title = 'With SEQUENCE:'
; PV-WAVE prints the following:
; With SEQUENCE:
; ( 0.773756, -0.106925)
; ( 0.400001, 0.158598)
; ( 0.0867063, 0.0920276)
; ( 0.00844932, 0.0239868)
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.