ANCOVAR Function (PV-WAVE Advantage)

IMSL Statistics Reference Guide > Analysis of Variance and Designed Experiments > ANCOVAR Function (PV-WAVE Advantage)

Analyzes a one-way classification model with covariates.

Usage

result = ANCOVAR (ni, y, x)

Input Parameters

ni—Array of length ngroup containing the number of responses for each group, where ngroup is the number of treatment groups..

y—Array of length n containing the data for the response variable where n = TOTAL(ni).

x—Array of size n by ncov containing the data for the covariates, where ncov is the number of covariates.

Returned Value

result—An array of length 15 containing the one-way analysis of covariance assuming parallelism, organized as follows:

0—Degrees of freedom for model (groups + covariates).

1—Degrees of freedom for error.

2—Total (corrected) degrees of freedom.

3—Sum of squares for model (groups and covariates combined).

4—Sum of squares for error.

5—Total (corrected) sum of squares.

6—Model mean square (groups and covariates combined).

7—Error mean square.

8—F-statistic.

9—p-value.

10—R2 (in percent).

11—Adjusted R2 (in percent).

12—Estimate of the standard deviation.

13—Overall response mean.

14—Coefficient of variation (in percent).

Input Keywords

Double—If present and nonzero, then double precision is used.

Output Keywords

Nmiss—The number of cases with missing values in x or y is returned in Nmiss. Cases with any missing values are not used in the analysis.

Adj_anova—Array of length 8 containing the partial sum of squares for the one-way analysis of covariance organized as follows:

Table 5-18: Partial Sum of Squares for the One-way Analysis of Covariance
i	Adj_anova(i)
0	Degrees of freedom for groups after covariates.
1	Degrees of freedom for covariates after groups.
2	Sum of squares for groups after covariates.
3	Sum of squares for model (groups and covariates combined).
4	F -statistic for groups.
5	F -statistic for covariates.
6	p-value for groups.
7	p-value for covariates.

Testpl—Array of length 10 containing the parallelism tests for the one-way analysis of covariance organized as follows:

Table 5-19: Parallelism Tests for the One-way Analysis of Covariance
i	testpl(i)
0	Extra degrees of freedom for model not assuming parallelism.
1	Degrees of freedom for error for model not assuming parallelism.
2	Degrees of freedom for error for model assuming parallelism.
3	Extra sum of squares for model not assuming parallelism.
4	Sum of squares for error for model not assuming parallelism.
5	Sum of squares for error for model assuming parallelism.
6	Mean square for testpl(0).
7	Mean square for testpl(1).
8	F-statistic.
9	p-value.

Xymean—Array of size ngroup+1 by ncov+3 containing the unadjusted means for the covariates and the response variate and the means for the response variate adjusted for the covariates. Each row for i = 0, 1, ..., ngroup – 1 corresponds to a group. Row ngroup contains overall statistics. The means are organized in Xymean columns as follows:

Table 5-20: Xymean Column Means
Column	Description
0	Number of non-missing cases
1 through ncov	Covariate means.
ncov + 1	Response mean.
ncov + 2	Response mean adjusted assuming parallelism.

Coef—Array of size ngroup + ncov by 4 containing statistics for the regression coefficients for the model assuming parallelism. Each row corresponds to a coefficient in the model. For i = 0, 1, ..., ngroup–1, row i is for the y intercept for the ith group. The remaining ncov rows are for the covariate coefficients. The statistics in the columns are organized as follows:

0—Coefficient estimate.

1—Estimated standard error of the estimate.

2—t-statistic.

3—p-value.

Co_tables—Array of size ngroup by ncov+1 by 4 containing statistics for a linear regression model fitted separately for each of the ngroup treatment groups. Each row corresponds to one of the ngroup treatment groups. Each column corresponds to the model coefficients. For column = 0, the statistics relate to the intercept in the regression model. For column = 1, 2, ..., ncov, the statistics relate to the slopes for the covariates. The third dimension corresponds to the columns described for Coef as follows:

0—Coefficient estimate.

1—Estimated standard error of the estimate.

2—t-statistic.

3—p-value.

Anova_tables—Array of size ngroup by 15 containing the analysis of variance tables for each linear regression model fitted separately to each treatment group. The 15 values in the ith row are for treatment group i organized as follows:

Table 5-21: Values for Treatment Group i
j	Anova_tables(i,j)
0	Degrees of freedom for regression model (covariates).
1	Degrees of freedom for error.
2	Total (corrected) degrees of freedom.
3	Sum of squares for regression model.
4	Sum of squares for error.
5	Total (corrected) sum of squares.
6	Model mean square.
7	Error mean square.
8	F-statistic.
9	p-value.
10	R2 (in percent).
11	Adjusted R2 (in percent).
12	Error standard deviation.
13	Overall response mean.
14	Coefficient of variation (in percent).

R_matrix—Array of size ngroup + ncov by ngroup + ncov containing the R matrix from the QR decomposition. The R matrix is from the regression assuming parallelism.

Covmeans—Array of size ngroup by ngroup containing the estimated matrix of variances and covariances for the adjusted means assuming parallelism.

Covcoef—Array of size ngroup + ncov by ngroup + ncov containing the estimated matrix of variances and covariances for the coefficients in Coef returned using Coef.

Discussion

The ANCOVAR function performs analyses for models that combine the features of a one-way analysis of variance model with that of a multiple linear regression model. The basic one-way analysis of covariance model is:

yij = β0i + β1xij1 + β2xij2 + ... + βmxijm + εij i = 1, 2, ..., ngroup; j = 1, 2, ... ni

where the observed value of yij constitutes the jth response in the ith group, β0i denotes the y intercept for the regression function for the ith group, β1, β2, ..., βm are the regression coefficients for the covariates, and the εij’s are independently distributed normal errors with mean zero and variance σ2. This model allows the regression function for each group to have different intercepts. However, the remaining m regression coefficients are the same for each group, i.e., the regression functions are parallel.

In practice, sometimes the regression functions are not parallel. In addition to estimates for the model assuming parallelism, ANCOVAR computes estimates and summary statistics for the separate regressions for each group. These estimates can be examined using the Co_tables and Anova_tables keywords.

Estimates for the β0i’s and β1, β2, ..., βm in the model assuming parallelism are returned using the Coef keyword. Summary statistics are also computed for this model.

The adjusted group means, stored in the last column of Xymean, are computed using the formula:

The estimated covariance between the i1th and i2th adjusted group mean is given by:

where vpq is the entry in covb((p - 1)(ngroup + ncov) + q – 1) and is the estimated covariance between the pth and qth estimated coefficients in the regression function.

A discussion of formulas and interpretations for the one-way analysis of covariance problem appears in most elementary statistics texts, e.g., Snedecor and Cochran (1967, Chapter 14).

Example 1

This example fits a one-way analysis of covariance model assuming parallelism using data discussed by Snedecor and Cochran (Table 14.6.1, pages 432−436). The responses are concentrations of cholesterol (in mg/100 ml) in the blood of two groups of women: women from Iowa and women from Nebraska. Age of a woman is the single covariate. The cholesterol concentrations and ages of the women according to state are shown in the following table. (11 Iowa women and 19 Nebraska women are in the study. Only the first 5 women from each state are shown here.)

Table 5-22: Age and Cholesterol Concentrations
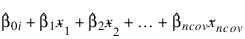
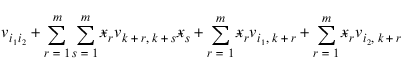
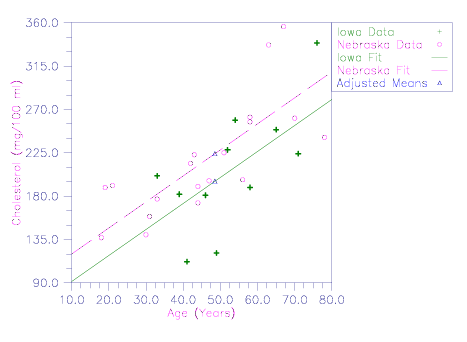
Iowa		Nebraska
Age	Cholesterol	Age	Cholesterol
46	181	18	137
52	228	44	173
39	182	33	177
65	249	78	241
54	259	51	225

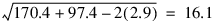
There is no evidence from the data to indicate that the regression lines for cholesterol concentration as a function of age are not parallel for Iowa and Nebraska women (p-value is 0.5425). The parallel line model suggests that Nebraska women may have higher cholesterol concentrations than Iowa women. The cholesterol concentrations (adjusted for age) are 195.5 for Iowa women versus 224.2 for Nebraska women. The difference is 28.7 with an estimated standard error of:

PRO t_ancovar_ex1

  ncov=1

  ngroup=2

  ni = [11, 19]

  nobs = TOTAL(ni)

  y =  $

  [181.0, 228.0, 182.0, 249.0, 259.0,$

   201.0, 121.0, 339.0, 224.0, 112.0,$

   189.0, 137.0, 173.0, 177.0, 241.0,$

   225.0, 223.0, 190.0, 257.0, 337.0,$

   189.0, 214.0, 140.0, 196.0, 262.0,$

   261.0, 356.0, 159.0, 191.0, 197.0]

 x = $   ; Should be nobs x ncov.

  [46.0, 52.0, 39.0, 65.0, 54.0,$

   33.0, 49.0, 76.0, 71.0, 41.0,$

   58.0, 18.0, 44.0, 33.0, 78.0,$

   51.0, 43.0, 44.0, 58.0, 63.0,$

   19.0, 42.0, 30.0, 47.0, 58.0,$

   70.0, 67.0, 31.0, 21.0, 56.0]

   aov = ANCOVAR(ni, y, x,$

         Testpl=testpl,   $

         Xymean=xymean,   $

         Covmeans=covm)

  PRINT,"             * * * ANALYSIS OF VARIANCE * * * "

  PRINT,"                  Sum of         Mean                Prob of"

  PRINT,"Source   DF      Squares        Square    Overall F"+ $

     "  Larger F"

  PRINT,"Model    ",STRING(aov(0),Format="(f3.0)"),"  ",$

        STRING(aov(3),Format="(f10.2)"),"      ",$

        STRING(aov(6),Format="(f9.2)")," ",$

        STRING(aov(8),Format="(f8.2)"),"     ",$

        STRING(aov(9),Format="(f8.6)")

  PRINT,"Error    ",STRING(aov(1),Format="(f3.0)"),"  ",$

        STRING(aov(4),Format="(f10.2)"),"     ",$

        STRING(aov(7),Format="(f9.2)")

  PRINT,"Total    ",STRING(aov(2),Format="(f3.0)"),"  ",$

         STRING(aov(5),Format="(f10.2)")

  PRINT,""

  PRINT,"             * * * TEST FOR PARALLELISM  * * * "

  PRINT,"                      Sum of     Mean         F     Prob of"

  PRINT,"SOURCE          DF    Squares   Square       TEST   Larger F"

  PRINT,"Extra due to"

  PRINT,"Nonparallelism   ",STRING(testpl(0), $

         Format="(f3.0)"),"",$

         STRING(testpl(3),Format="(f10.2)"),"  ",$

         STRING(testpl(6),Format="(f7.2)"),"     ",$

         STRING(testpl(8),Format="(f7.5)")," ",$

         STRING(testpl(9),Format="(f8.4)")

  PRINT,"Extra Assuming"

  PRINT,"Nonparallelism   ",STRING(testpl(1),$

         Format="(f3.0)"),"",$

         STRING(testpl(4),Format="(f10.2)"),"  ",$

         STRING(testpl(7),Format="(f7.2)")

  PRINT,"Error Assuming"

  PRINT,"Parallelism      ",STRING(testpl(2),$

         Format="(f3.0)"),"",$

         STRING(testpl(5),Format="(f10.2)")

  PRINT,""

  PRINT,"            XY Mean Matrix"

  PRINT,"        1         2         3         4"

  FOR i=0L, ngroup DO BEGIN

    PRINT,STRTRIM(i+1,2),"  ",$

          STRING(xymean(i,0),Format="(f6.1)"),"    ",$

          STRING(xymean(i,1),Format="(f6.1)"),"    ",$

          STRING(xymean(i,2),Format="(f6.1)"),"    ",$

          STRING(xymean(i,3),Format="(f6.1)")

  ENDFOR

  PRINT,""

  PRINT,"  Var./Covar. Matrix of Adjusted Group Means"

  PRINT,"                 1             2"

  FOR i=0L, ngroup-1 DO BEGIN

    PRINT,"      ",STRTRIM(i+1,2),"     ",$

         STRING(covm(i,0),Format="(f6.1)"),"        ",$

         STRING(covm(i,1),Format="(f6.1)")

  ENDFOR

END

Output

            * * * ANALYSIS OF VARIANCE * * *

                  Sum of         Mean                Prob of

Source   DF      Squares        Square    Overall F  Larger F

Model     2.    54432.76       27216.38    14.97     0.000042

Error    27.    49103.90       1818.66

Total    29.   103536.66

             * * * TEST FOR PARALLELISM  * * *

                       Sum of     Mean         F     Prob of

SOURCE           DF    Squares   Square       TEST   Larger F

Extra due to

Nonparallelism    1.    709.04   709.04     0.38093   0.5425

Extra Assuming

Nonparallelism   26.  48394.87  1861.34

Error Assuming

Parallelism      27.  49103.90

            XY Mean Matrix

        1         2         3         4

1    11.0      53.1     207.7     195.5

2    19.0      45.9     217.1     224.2

3    30.0      48.6     213.7     213.7

  Var./Covar. Matrix of Adjusted Group Means

                 1             2

      1      170.4          -2.9

      2       -2.9          97.4

Figure 5-3: Plot of Cholesterol Concentrations and Fitted Parallel Lines by State

Example 2

This example fits a one-way analysis of covariance model and performs a test for parallelism using data discussed by Snedecor and Cochran (1967, Table 14.8.1, pages 438–443). The responses are weight gains (in pounds per day) of 40 pigs for four groups of pigs under varying treatments. Two covariates-initial age (in days) and initial weight (in pounds) are used. For each treatment, there are 10 pigs. Only the first 5 pigs from each treatment are shown here.

Table 5-23: Weight Gains per Treatment
Treatment 1			Treatment 2			Treatment 3			Treatment 4
Age	Wt.	Gain	Age	Wt.	Gain	Age	Wt.	Gain	Age	Wt.	Gain
78	61	1.40	78	74	1.61	78	80	1.67	77	62	1.40
90	59	1.79	99	75	1.31	83	61	1.41	71	55	1.47
94	76	1.72	80	64	1.12	79	62	1.73	78	62	1.37
71	50	1.47	75	48	1.35	70	47	1.23	70	43	1.15
99	61	1.26	94	62	1.29	85	59	1.49	95	57	1.22

For this data, the test for non-parallelism is not statistically significant (p = 0.901). The one-way analysis of covariance test for the treatment means adjusted for the covariates, assuming parallel slopes, is statistically significant at a stated significance level of α = 0.05, (p = 0.04931).

Multiple comparisons can be done using the least significant difference approach of comparing each pair of treatment groups with the two-sample student-t test. Since the adjusted means in the one-way analysis of covariance are correlated, the standard error for these comparisons must be computed using the variances and covariances in Covmeans. The standard errors for these comparisons are fairly similar ranging from 0.0630 to 0.0638. The Student’s t comparisons identify differences between groups 1 and 2, and 1 and 4 as being statistically significant with p-values of 0.01225 and 0.03854 respectively.

PRO t_ancovar_ex2

  ncov=2

  ngroup=4

  ni = [10, 10, 10, 10]

  nobs = SUM(ni)

  x1 = $

  [78.0, 90.0, 94.0, 71.0, 99.0, 80.0, 83.0, 75.0, 62.0, 67.0,$

   78.0, 99.0, 80.0, 75.0, 94.0, 91.0, 75.0, 63.0, 62.0, 67.0,$

   78.0, 83.0, 79.0, 70.0, 85.0, 83.0, 71.0, 66.0, 67.0, 67.0,$

   77.0, 71.0, 78.0, 70.0, 95.0, 96.0, 71.0, 63.0, 62.0, 67.0]

  x2 = $

  [61.0, 59.0, 76.0, 50.0, 61.0, 54.0, 57.0, 45.0, 41.0, 40.0,$

   74.0, 75.0, 64.0, 48.0, 62.0, 42.0, 52.0, 43.0, 50.0, 40.0,$

   80.0, 61.0, 62.0, 47.0, 59.0, 42.0, 47.0, 42.0, 40.0, 40.0,$

   62.0, 55.0, 62.0, 43.0, 57.0, 51.0, 41.0, 40.0, 45.0, 39.0]

  y = $

  [1.40, 1.79, 1.72, 1.47, 1.26, 1.28, 1.34, 1.55, 1.57, 1.26,$

   1.61, 1.31, 1.12, 1.35, 1.29, 1.24, 1.29, 1.43, 1.29, 1.26,$

   1.67, 1.41, 1.73, 1.23, 1.49, 1.22, 1.39, 1.39, 1.56, 1.36,$

   1.40, 1.47, 1.37, 1.15, 1.22, 1.48, 1.31, 1.27, 1.22, 1.36]

  x=FLTARR(nobs,ncov)

  ; Set up covariate input matrix.

  x(*,0) = x1

  x(*,1) = x2

    aov = ANCOVAR(ni, y, x, $

               Testpl=testpl, $

               Adj_anova=adj_aov, $

               Xymean=xymean, $

               Covmeans=covm)

  PRINT,""

  PRINT,"             * * * TEST FOR PARALLELISM  * * * "

  PRINT,"                        Sum of     Mean         F     Prob of"

  PRINT,"SOURCE           DF     Squares   Square       TEST"+$

        "   Larger F"

  PRINT,"Extra due to"

  PRINT,"Nonparallelism  ",STRING(testpl(0),$

         Format="(f3.0)")," ",$

         STRING(testpl(3),Format="(f10.2)"),"   ",$

         STRING(testpl(6),Format="(f7.2)"),"    ",$

         STRING(testpl(8),Format="(f7.5)"),"  ",$

         STRING(testpl(9),Format="(f7.4)")

  PRINT,"Extra Assuming"

  PRINT,"Nonparallelism   ",STRING(testpl(1),$

         Format="(f3.0)"),"",$

         STRING(testpl(4),Format="(f10.2)"),"   ",$

         STRING(testpl(7),Format="(f7.2)")

  PRINT,"Error Assuming"

  PRINT,"Parallelism      ",STRING(testpl(2),$

         Format="(f3.0)"),"",$

         STRING(testpl(5),Format="(f10.2)")

  PRINT,""

  PRINT,"             * * * ANALYSIS OF VARIANCE * * * "

  PRINT,"                Sum of     Mean                  Prob of"

  PRINT,"Source   DF    Squares    Square    Overall F"+$

        "    Larger F"

  PRINT,"Model   ",STRING(aov(0),Format="(f3.0)")," ",$

        STRING(aov(3),Format="(f10.5)")," ",$

        STRING(aov(6),Format="(f9.5)"),"    ",$

        STRING(aov(8),Format="(f9.5)"),"    ",$

        STRING(aov(9),Format="(f8.6)")

  PRINT,"Error   ",STRING(aov(1),Format="(f3.0)")," ",$

        STRING(aov(4),Format="(f10.5)")," ",$

        STRING(aov(7),Format="(f9.5)")

  PRINT,"Total   ",STRING(aov(2),Format="(f3.0)")," ",$

         STRING(aov(5),Format="(f10.5)")

  PRINT,""

  PRINT,""

  PRINT,"         * * * ADJUSTED ANALYSIS OF VARIANCE  * * * "

  PRINT,"                                Sum of     F     Prob of"

  PRINT,"Source                    DF    Squares   TEST   Larger F"

  PRINT,"Groups after Covariates  ",STRING(adj_aov(0),$

        Format="(f3.0)"),"",$

        STRING(adj_aov(2),Format="(f10.2)"),"  ",$

        STRING(adj_aov(4),Format="(f5.2)"),"    ",$

        STRING(adj_aov(6),Format="(f7.5)")

  PRINT,"Covariates after Groups  ",STRING(adj_aov(1),$

        Format="(f3.0)"),"",$

        STRING(adj_aov(3),Format="(f10.2)"),"  ",$

        STRING(adj_aov(5),Format="(f5.2)"),"    ",$

        STRING(adj_aov(7),Format="(f7.5)")

  PRINT,""

  PRINT,"           * * * GROUP MEANS * * * "

  PRINT,"GROUP  | Unadjusted   |  Adjusted |  Std. Error"

  FOR i=0L, ngroup-1 DO BEGIN

    stderr = SQRT(covm(i,i))

    PRINT, STRTRIM(i+1,2),"      | ", $

           STRING(xymean(i, ngroup-1),Format="(f7.4)"),"      | ",$

           STRING(xymean(i, ngroup ),Format="(f7.4)"),"   | ",$

           STRING(stderr,Format="(f7.4)")

  ENDFOR

  PRINT,""

  PRINT,"      * * * STUDENT-T MULTIPLE COMPARISONS * * * "

  PRINT," GROUPS  |    DIFF   | Std. Error | Student-t | P-Value"

  FOR i=0L, ngroup-1 DO BEGIN

    FOR j=i+1, ngroup-1 DO BEGIN

      delta  = xymean(i,ngroup) - $

               xymean(j,ngroup)

      stderr = SQRT(covm(i,i)+covm(j,j)- $

               2.0*covm(i,j))

      t      = delta/stderr;

      df     = xymean(i,0)+xymean(j,0)-2

      pvalue = 1.0 - TCDF(t, df)

      PRINT, STRTRIM(i+1,2)," vs ",STRTRIM(j+1,2),"   | ",$

               STRING(delta,Format="(f7.4)"),"   | ",$

               STRING(stderr,Format="(f7.4)"),"    | ",$

               STRING(t,Format="(f7.3)"),"   | ",$

               STRING(pvalue,Format="(f7.5)")

    ENDFOR

  ENDFOR

END

Output

* * * TEST FOR PARALLELISM  * * *

                        Sum of     Mean         F     Prob of

SOURCE           DF     Squares   Square       TEST   Larger F

Extra due to

Nonparallelism   6.       0.05      0.01    0.35534   0.9007

Extra Assuming

Nonparallelism   28.      0.62      0.02

Error Assuming

Parallelism      34.      0.67

             * * * ANALYSIS OF VARIANCE * * *

                Sum of     Mean                  Prob of

Source   DF    Squares    Square    Overall F    Larger F

Model    5.    0.35252   0.07050      3.57640    0.010491

Error   34.    0.67026   0.01971

Total   39.    1.02278

         * * * ADJUSTED ANALYSIS OF VARIANCE  * * *

                                Sum of     F     Prob of

Source                    DF    Squares   TEST   Larger F

Groups after Covariates   3.      0.17   2.90    0.04931

Covariates after Groups   2.      0.17   4.44    0.01939

           * * * GROUP MEANS * * *

GROUP  | Unadjusted   |  Adjusted |  Std. Error

1      |  1.4640      |  1.4614   |  0.0448

2      |  1.3190      |  1.3068   |  0.0446

3      |  1.4450      |  1.4429   |  0.0447

4      |  1.3250      |  1.3418   |  0.0449

      * * * STUDENT-T MULTIPLE COMPARISONS * * *

 GROUPS  |    DIFF   | Std. Error | Student-t | P-Value

1 vs 2   |  0.1546   |  0.0630    |   2.455   | 0.01225

1 vs 3   |  0.0185   |  0.0637    |   0.290   | 0.38750

1 vs 4   |  0.1196   |  0.0638    |   1.875   | 0.03854

2 vs 3   | -0.1362   |  0.0632    |  -2.153   | 0.97743

2 vs 4   | -0.0350   |  0.0638    |  -0.549   | 0.70528

3 vs 4   |  0.1011   |  0.0631    |   1.602   | 0.06330

Version 2017.0