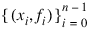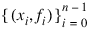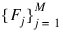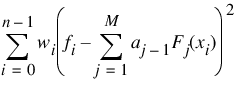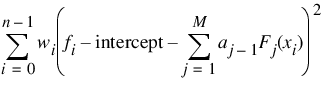FCNLSQ Function (PV-WAVE Advantage)
Computes a least-squares fit using user-supplied functions.
Usage
result = FCNLSQ(f, nbasis, xdata, fdata)
Input Parameters
f—Scalar string specifying the name of a user-supplied function that defines the subspace from which the least-squares fit is to be performed. The k-th basis function evaluated at x is f (k, x), where k = 1, 2, ..., nbasis.
nbasis—Number of basis functions.
xdata—One-dimensional array containing the abscissas of the least-squares problem.
fdata—One-dimensional array containing the ordinates of the least-squares problem.
Returned Value
result—A one-dimensional array containing the coefficients of the basis functions.
Input Keywords
Double—If present and nonzero, double precision is used.
Weights—Array of weights used in the least-squares fit.
Output Keywords
Intercept—Named variable into which the coefficient of a constant function used to augment the user-supplied basis functions in the least-squares fit is stored. Setting this keyword forces an intercept to be added to the model.
SSE—Named variable into which the error sum of squares is stored.
Discussion
For a discussion of the principles relating to the implementation of FCNLSQ, refer to the discussion of FCNLSQ in the PV‑WAVE IMSL Mathematics Reference.
Function FCNLSQ computes a best least-squares approximation to given univariate data of the form:
by M basis functions:
(where M = nbasis). In particular, the default for this function returns the coefficients a which minimize:
where w = Weights, n = N_ELEMENTS (xdata), x = xdata, and f = fdata.
If optional argument Intcercept is chosen, then an intercept is placed in the model and the coefficients a, returned by FCNLSQ, minimize the error sum of squares as indicated below.
Example
In this example, the following function is fit:
1 + sinx + 7sin3x
This function is evaluated at 90 equally spaced points on the interval [0, 6]. Four basis functions, 1, sinx, sin2x, and sin3x, are used.
.RUN
; Define the basis functions.
- FUNCTION f, k, x
- IF (k EQ 1) THEN RETURN, 1. $
- ELSE RETURN, SIN((k - 1) * x)
- END
% COMPILED module: F.
n = 90
; Generate the data.
xdata = 6 * FINDGEN(n)/(n - 1)
fdata = 1 + SIN(xdata) + 7 * SIN(3 * xdata)
nbasis = 4
coefs = FCNLSQ('f', nbasis, xdata, fdata); Compute the coefficients summing FCNLSQ.
PM, coefs, Format = '(f10.5)'
; Print the results.
; 1.00000
; 1.00000
; 0.00000
; 7.00000
Warning Errors
MATH_LINEAR_DEPENDENCE—Linear dependence of the basis functions exists. One or more components of coef are set to zero.
MATH_LINEAR_DEPENDENCE_CONST—Linear dependence of the constant function and basis functions exists. One or more components of coef are set to zero.
Fatal Errors
MATH_NEGATIVE_WEIGHTS_2—All weights must be greater than or equal to zero.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.