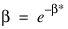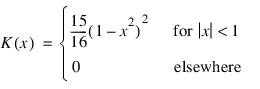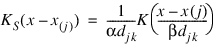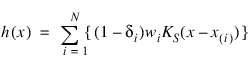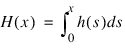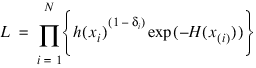NONPARAM_HAZARD_RATE Function (PV-WAVE Advantage)
Performs nonparametric hazard rate estimation using kernel functions and quasi-likelihoods.
Usage
result = nonparam_hazard_rate (t, n_hazard, hazard_min, hazard_increment)
Input Parameters
t—Array of n_observations containing the failure times, where n_observations is the number of observations. If the Censor_codes keyword is used, the values of t may be treated as exact failure times, as right-censored times, or a combination of exact and right censored times. By default, all times in t are assumed to be exact failure times.
n_hazard—Number of grid points the hazard is computed at. The function computes the hazard rates over the range given by: Hazard_min + j * Hazard_increment, for j = 0, ..., n_hazard – 1.
hazard_min—First grid value.
hazard_increment—Increment between grid values.
Returned Value
result—Array of length n_hazard containing the estimated hazard rates.
Input Keywords
Double—If present and nonzero, double precision is used.
Censor_codes—Array of length n_observations containing the censoring codes for each time in t. If Censor_codes(i) = 0 the failure time t(i) is treated as an exact time of failure. Otherwise it is treated as a right-censored time; that is, the exact time of failure is greater than t(i). Default: All failure times are treated as exact times of failure with no censoring.
Weight_option—Weight option. If Weight_option = 1, then weight = ln(1 + 1/(n_observations – i)) is used for the ith smallest observation. Otherwise, weight = 1/(n_observations – i) is used. Default: Weight_option = 0.
Sort_option—Sorting option. If Sort_option = 1, then the event times are not automatically sorted by the function. Otherwise, sorting is performed with exact failure times following tied right-censored times. Default: Sort_option = 0.
note | The keywords N_k_grid, K_start, and K_increment must be used together if any of them are supplied as inputs to NONPARAM_HAZARD_RATE. This set of keywords is used to find the optimal value of k over the range given by: K_start + (j – 1) * K_increment, for j = 1, ..., N_k_grid The value of k used here is the number of nearest neighbors to be used in computing the k-th nearest neighbor distance. See the Discussion section for more details. |
N_k_grid—The number of values of k to be considered. Default: N_k_grid will be at most 10 points.
K_start—The minimum value for k. Default: smallest possible value of k.
K_increment—The increment between successive values of k. Default: K_increment = 2.
note | The keywords N_beta_grid, Beta_start, and Beta_increment must be used together if any of them are supplied as inputs to NONPARAM_HAZARD_RATE. This set of keywords allows for a user-defined grid where: Beta_start + (j – 1)*Beta_increment, for j = 1, ..., N_beta_grid The values in the initial beta search are given as follows: Let β = –8, –4, –2, –1, –0.5, 0.5, 1, and 2; and: For each value of β, Optimal_criterion is computed at the optimizing β. The maximizing β is used to initiate the iterations. If the initial β* is determined from the search to be less than –6, then it is presumed that β is infinite, and an analytic estimate of α based upon infinite β is used. Infinite β corresponds to a flat hazard rate. |
N_beta_grid—If N_beta_grid is present and > 0, use a user-defined grid.
Beta_start—The first value to be used in the user-defined grid.
Beta_increment—The increment value between successive grid values.
Output Keywords
N_missing—Number of missing (NaN, not a number) failure times in t.
Optimal_alpha—Optimal estimate for the parameter α.
Optimal_beta—Optimal estimate for the parameter β.
Optimal_criterion—Optimum value of the criterion function.
Optimal_k—Optimal estimate for the parameter k.
Sorted_event_times—Array of length n_observations containing the times of occurrence of the events, sorted from smallest to largest.
Sorted_censor_codes—Array of length n_observations containing the sorted censor codes. Censor codes are sorted corresponding to the events Sorted_event_times(i), with censored observations preceding tied failures.
Discussion
NONPARAM_HAZARD_RATE is an implementation of the methods discussed by Tanner and Wong (1984) for estimating the hazard rate in survival or reliability data with right censoring. It uses the biweight kernel:
and a modified likelihood to obtain data-based estimates of the smoothing parameters α, β, and k needed in the estimation of the hazard rate. For kernel K(x), define the “smoothed” kernel Ks(x – x(j)) as follows:
where djk is the distance to the kth nearest failure from x(j), and x(j) is the jth ordered observation (from smallest to largest). For given α and β, the hazard at point x is then:
where N = n_observations, δi is the ith observation’s censor code (1 = censored, 0 = failed), and wi is the ith ordered observation’s weight, which may be chosen as either 1/(N – i + 1), or ln(1 + 1/(N – i + 1)). Let:
The likelihood is given by:
where Π denotes product. Since the likelihood leads to degenerate estimates, Tanner and Wong (1984) suggest the use of a modified likelihood. The modification consists of deleting observation xi in the calculation of h(xi) and H(xi) when the likelihood term for xi is computed using the usual optimization techniques. α and β for given k can then be estimated.
Estimates for α and β are computed as follows: for given β, a closed form solution is available for α. The problem is thus reduced to the estimation of β. A grid search for β is first performed. Experience indicates that if the initial estimate of β from this grid search is greater than, say, e6, then the modified likelihood is degenerate because the hazard rate does not change with time. In this situation, β should be taken to be infinite, and an estimate of α corresponding to infinite β should be directly computed. When the estimate of β from the grid search is less than e6, a secant algorithm is used to optimize the modified likelihood. The secant algorithm iteration stops when the change in β from one iteration to the next is less than 10-5. Alternatively, the iterations may cease when the value of β becomes greater than e6, at which point an infinite β with a degenerate likelihood is assumed.
To find the optimum value of the likelihood with respect to k, a user-specified grid of k-values is used. For each grid value, the modified likelihood is optimized with respect to α and β. That grid point, which leads to the smallest likelihood, is taken to be the optimal k.
Programming Notes
1. If sorting of the data is performed by NONPARAM_HAZARD_RATE, then the sorted array will be such that all censored observations at a given time precede all failures at that time. To specify an arbitrary pattern of censored/failed observations at a given time point, the Sort_option keyword must be set. In this case, it is assumed that the times have already been sorted from smallest to largest.
2. The smallest value of k must be greater than the largest number of tied failures since djk must be positive for all j. (Censored observations are not counted.) Similarly, the largest value of k must be less than the total number of failures. If the grid specified for k includes values outside the allowable range, then a warning error is issued; but k is still optimized over the allowable grid values.
3. The secant algorithm iterates on the transformed parameter β* = exp(–β). This assures a positive β, and it also seems to lead to a more desirable grid search. All results returned to the user are in the original parameterization, however.
4. Since local minimums have been observed in the modified likelihood, it is recommended that more than one grid of initial values for α and β be used.
5. Function NONPARAM_HAZARD_RATE assumes that the hazard grid points are new data points.
Example
The following example is taken from Tanner and Wong (1984). The data is from Stablein, Carter, and Novak (1981) and involve the survival times of individuals with nonresectable gastric carcinoma. Only individuals treated with both radiation and chemotherapy are used. For each value of k from 18 to 22 with increment of 2, the default grid search for β is performed. Using the optimal value of β in the grid, the optimal parameter estimates of α and β are computed for each value of k. The final solution is the parameter estimates for the value of k which optimizes the modified likelihood (Optimal_criterion).
; Number of observations.
n_observations = 45
; The minimum value for parameter k.
kmin = 18
; The increment between successive values of parameter k.
increment_k = 2
; The number of values of k to be considered.
n_k = 3
; Sorting option
isort = 1
; Number of grid points at which to compute the hazard.
n_hazard = 100
; First grid value
hazard_min = 0.0
; Increment between grid values.
hazard_inc = 10
; An array of n_observations containing the failure times.
t = [ 17.0, 42.0, 44.0, 48.0, 60.0, 72.0, 74.0, 95.0, $
103.0, 108.0, 122.0, 144.0, 167.0, 170.0, 183.0, $
185.0, 193.0, 195.0, 197.0, 208.0, 234.0, 235.0, $
254.0, 307.0, 315.0, 401.0, 445.0, 464.0, 484.0, $
528.0, 542.0, 567.0, 577.0, 580.0, 795.0, 855.0, $
882.0, 892.0,1031.0,1033.0,1306.0,1335.0,1366.0, $
1452.0, 1472.0]
; An array of length n_observations containing the
; censoring codes for each time in t.
censor_codes=[ 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, $
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, $
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, $
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, $
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
; Call the NONPARAM_HAZARD_RATE routine
haz = NONPARAM_HAZARD_RATE(t, n_hazard, $
hazard_min, hazard_inc, $
N_k_grid=n_k, $
K_start=kmin, $
K_increment=increment_k, $
N_missing=n_missing, $
Sort_option=isort, $
Censor_codes=censor_codes, $
Sorted_event_times=sorted_event_times, $
Sorted_censor_codes=sorted_censor_codes, $
Optimal_criterion=criterion, $
Optimal_k=optimal_k, optimal_alpha=optimal_alpha, $
Weight=0, optimal_beta=optimal_beta, $
N_beta_grid=0, beta_start=0.0, $
Beta_increment=0.0)
; Format the output
PRINT, ""
PRINT," *** Optimal parameter estimates ***"
PRINT," alpha beta k criterion"
PRINT, optimal_alpha, optimal_beta, optimal_k, criterion
PRINT, ""
PRINT, "nmiss = ", n_missing
PRINT, ""
PRINT," Sorted Event Times"
PRINT, sorted_event_times, Format = '(5F13.2)'
PRINT, ""
PRINT," Sorted Censors"
PRINT, sorted_censor_codes,Format = '(8I8)'
PRINT, ""
PRINT," Hazard Rates"
PRINT, haz, Format = '(5F13.6)'
Output
*** Optimal parameter estimates ***
alpha beta k criterion
1.54053 1.63155 20 -261.771
nmiss = 0
Sorted Event Times
17.00 42.00 44.00 48.00 60.00
72.00 74.00 95.00 103.00 108.00
122.00 144.00 167.00 170.00 183.00
185.00 193.00 195.00 197.00 208.00
234.00 235.00 254.00 307.00 315.00
401.00 445.00 464.00 484.00 528.00
542.00 567.00 577.00 580.00 795.00
855.00 882.00 892.00 1031.00 1033.00
1306.00 1335.00 1366.00 1452.00 1472.00
Sorted Censors
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1
1 1 1 1 1
Hazard Rates
0.000962 0.001111 0.001276 0.001451 0.001634
0.001819 0.002004 0.002185 0.002359 0.002523
0.002675 0.002813 0.002935 0.003040 0.003126
0.003193 0.003240 0.003266 0.003273 0.003260
0.003229 0.003179 0.003114 0.003034 0.002941
0.002838 0.002727 0.002612 0.002495 0.002381
0.002273 0.002175 0.002084 0.001998 0.001917
0.001841 0.001771 0.001709 0.001655 0.001608
0.001569 0.001537 0.001510 0.001484 0.001459
0.001435 0.001411 0.001388 0.001365 0.001343
0.001323 0.001304 0.001285 0.001266 0.001247
0.001228 0.001208 0.001188 0.001167 0.001146
0.001125 0.001103 0.001081 0.001060 0.001040
0.001020 0.000999 0.000979 0.000958 0.000936
0.000913 0.000891 0.000868 0.000845 0.000821
0.000798 0.000775 0.000752 0.000730 0.000708
0.000685 0.000662 0.000640 0.000617 0.000595
0.000573 0.000552 0.000530 0.000510 0.000490
0.000471 0.000452 0.000434 0.000416 0.000399
0.000383 0.000366 0.000351 0.000336 0.000321
Errors
STAT_ALL_OBSERVATIONS_MISSING—All observations are missing (NaN, not a number) values.
Version 2017.0
Copyright © 2017, Rogue Wave Software, Inc. All Rights Reserved.